C++机器学习（4）Logistic回归


Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383

Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383

Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383

部分资料下载地址： http://pan.baidu.com/s/1bpsgt5t 提取码fwxf
源码下载地址：https://github.com/fawdlstty/hm_ML

继续开始机器学习的研究。这次的内容叫Logistic回归。什么叫Logistic回归？直观理解就是，通过不断的迭代，使结果接近最优解。
如下图示例：
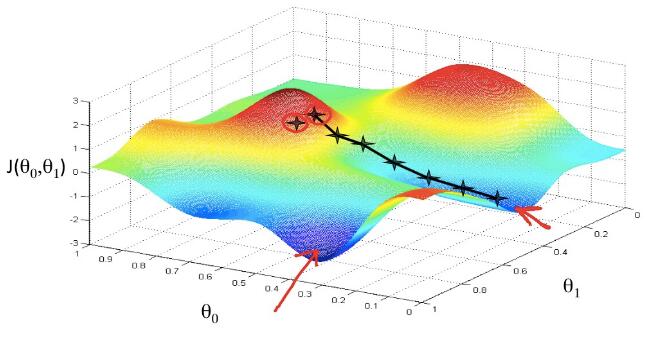
20160517120948
在由θ0、θ1以及J(θ0,θ1)组成的三维立体空间中，从最开始的山顶上，每走一步计算一下怎样走下山最快。通过不同的起点或不同的步长，甚至可以获得不同的结果，比如红色箭头所标注的位置。

下面可能就有人迷糊了。θ0、θ1、J(θ0,θ1)分别是什么鬼？下面我一一解释。
首先，在平面直角坐标系中，有一堆零散的点，如下图所示
20160517124247
上图的横轴和纵轴分别用x和y表示，我们需要知道空间中这堆零散的点之间的关系。然后，我们假设一个函数
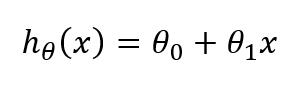
20160517123307
这个函数的θ0和θ1我们都不知道，现在我们先把这函数假设出来，接下来我们要通过算法使其越来越接近图示中黑色线。黑色分隔线的用处在于，一旦确定了这条线，以后需要根据x求得y的值，就非常方便了。比如根据面积预测房价等。
回到最上图，θ0、θ1的意思解释了，接下来说说J(θ0,θ1)是个什么鬼。在图中，我们需要求得三维空间中局部最低点，也就是J(θ0,θ1)最小的情况。为什么是最小呢？因为将这个三维转为二维，所假设的效果是，需要让所有点距黑线的距离最短。所以我们需要求得局部最低点。方程为：
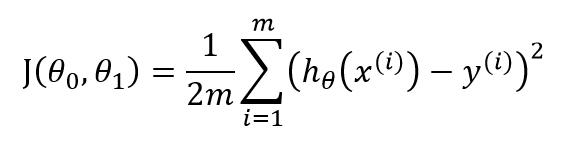
20160517124852
感觉难度瞬间上升一个档次哇？公式看起来是挺吓人的。公式的意思为，求得所有点距目标直线的平均距离。在首图中，平均距离很远代表山顶，平均距离很近代表山脚。我们通过不断的迭代求得山脚的位置也就是通过不断调整θ0、θ1两个参数从而使得J(θ0,θ1)越来越小的过程。这儿J(θ0,θ1)就叫代价函数。稍微解释一下公式的意思，貌似E这个符号代表累加，也就是i从1循环到m，把结果加起来然后除以2m；hθ也就是我们的假设函数，y代表求得的结果。平方为简化的计算方差。
从公式可以看出，如果我们的假设函数hθ越来越准，越来越接近y，那么我们的代价函数也将会越来越小。
然后是迭代的过程，即下图公式：
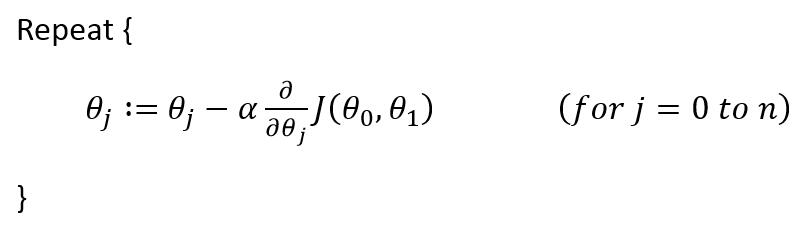
20160517130313
我们需要让θ0、θ1越来越接近标准，怎么做呢？就按照上图所示方法。这儿公式叫做批量梯度下降。这儿α代表步长∂/∂θj代表偏导数，这个概念有点难解释，大意是对其取偏导数使hθ接近准确答案。
将以上公式带入，公式将究极进化为如下形式：
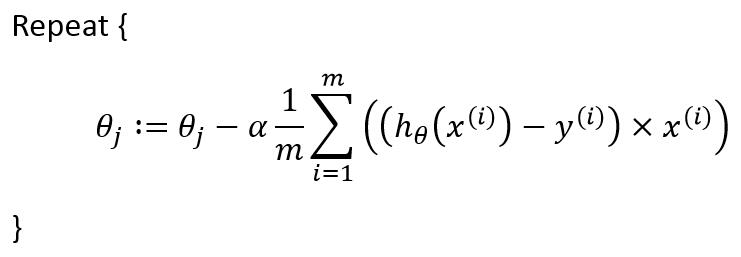
20160517131440
上面公式差不多可以直接写成代码咯。接下来就是代码的实现：

1
2
3
4

//回归循环次数
#define RUN_CYCLE_NUM 50000
//回归递增步长
#define ALPHA_NUM 0.001

上面两行主要是迭代次数与递增步长，这两个参数需要手工调试才能测出当前环境最优解。接下来是类的定义，由于编写这个类改动了以前的代码，为了方便，之前的文章不再重新更新代码，最终代码以百度云共享的代码为准。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Logistic : public Feature_Object_Collection <double> {
public:
    Logistic (std::initializer_list<Feature_Object<double>> list) : Feature_Object_Collection (list) {
        init_theta0 ();
    }
 
    Logistic (Feature_Object_Collection& o) : Feature_Object_Collection (o) {
        init_theta0 ();
    }
 
    Logistic (const Logistic &o) : Feature_Object_Collection (o) {}
 
    ...
 
private:
    //在每个数据的特征前加个1，代表θ0
    void init_theta0 () {
        for (Feature_Object<double> &d : data) {
            d.push_front (1);
        }
    }
};

由于有了θ0这个奇葩的存在，为了计算简便，直接在特征前加入一个新特征，值全为1。
接下来就是公式的实现，参考上面公式实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

void calc (std::vector<double> &theta/*θ*/) {
    //阶跃函数
    auto sigmoid = [] (double d) { return 1. / (1. + ::pow (2.7182818284590451, 0 - d)); };
 
    //构建theta，其中theta[0]代表θ0， theta[1]代表θ1，以此类推
    theta.clear ();
    ptrdiff_t i, j, k;
    theta.reserve (data [0].get_size ());
    for (i = 0; i < data [0].get_size (); ++i) theta.push_back (1);
 
    //矩阵计算中的临时变量
    std::vector<double> tmp;
    tmp.resize (get_size ());
    double d;
 
    //Logistic回归主循环
    for (i = 0; i < RUN_CYCLE_NUM; ++i) {
        for (j = 0; j < get_size (); ++j) {
            //Hypothesisθ = sigmoid(dataMatrix*weights)
            tmp [j] = 0;
            for (k = 0; k < data [0].get_size (); ++k) tmp [j] += data [j] [k] * theta [k];
            tmp [j] = sigmoid (tmp [j]);
 
            //error = (Hypothesisθ - labelMat)
            tmp [j] -= data [j].get_label ();
        }
 
        //weights = weights - alpha * dataMatrix.transpose () * error
        for (j = 0; j < data [0].get_size (); ++j) {
            d = 0;
            for (k = 0; k < get_size (); ++k) d += data [k] [j] * tmp [k];
            d *= ALPHA_NUM;
            theta [j] -= d;
        }
    }
}

实现不细讲了，就是上面公式。接下来测试函数运行结果：
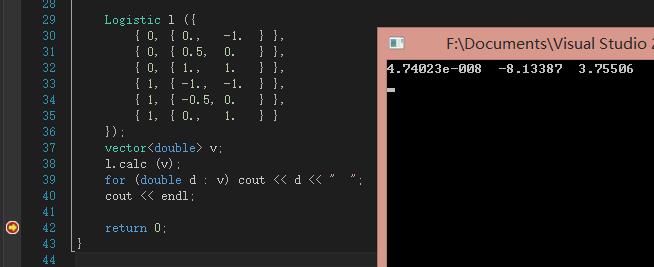
20160517132405
这儿的数值代表权值，或者叫重要程度。从比值可以看出，θ0可以忽略，θ1接近θ2的二倍。
上面的代码含有两个特征，大概类似于下图：
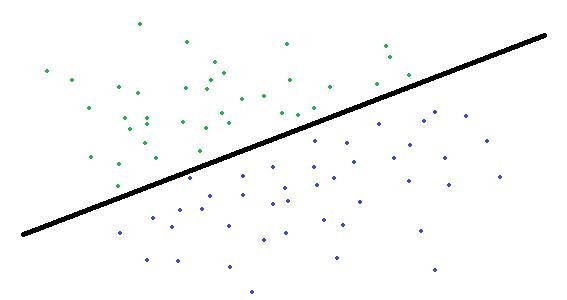
20160517122330
绿色和蓝色的点分别代表点的两种状态，横轴、纵轴分别代表点的两种特征，需要通过Logistic回归求得接近于黑线的分隔线（与上面公式只是多一个特征的差别）。通过迭代计算，算出的公式为如下形式，假设横轴、纵轴分别以x1与x2表示，那么公式为：
4.74023e-008 + (-8.13387*x1) + 3.75506*x2 = 0
上面我给出的几个测试数据非常简单，口算就能算出最优分隔线为(-2*x1)+x2=0，可见逻辑回归已经相当接近最优解了。
参考资料也在共享里面，除了ML/fawdlstty文件夹，其他全部是关于机器学习方面的资料。资料也不定期更新。

发布者

fawdlstty

又一只萌萌哒程序猿~~

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注