Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /www/wwwroot/fawdlstty.com/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
部分资料下载地址: http://pan.baidu.com/s/1bpsgt5t 提取码fwxf
源码下载地址:https://github.com/fawdlstty/hm_ML
M$大大前段时间弄了个小冰读心术,大概意思是通过15个问题,回答是、否、不知道,小冰就可以猜出你想的是什么人物。连接在这 微软小冰·读心术
这种逻辑非常像二叉决策树,通过递归(高手也可以用迭代)判断特征,最终确定目标类型。每次判断的分支有两种类型,一种是二叉决策树,一种是多叉决策树,它们之间并没有绝对的优劣之差,各自有各自的优点。
示例决策如下图所示:
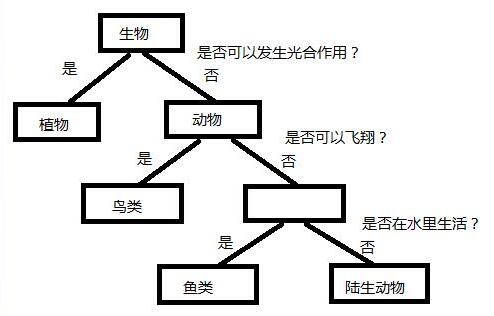
上图只是一个比较精简的决策的示例,可见决策树从速度上效率比之前的k-近邻算法强很多。实际上决策树也就是k-近邻算法的优化版,在损失一定精度情况下,可以使判断速度减少一个数量级。
接下来又到了一篇一次的贴代码时间。由于代码比较长,所以我将其划分成了几个部分:
1、定义决策树分支节点。这儿我选择的是多叉树。定义如下:
1 2 3 4 5 6 7 8 9 | struct Decision_Tree_Branch; typedef Decision_Tree_Branch *pDecision_Tree_Branch; struct Decision_Tree_Branch { ptrdiff_t feature_index; union { std::map<double, pDecision_Tree_Branch> *child; std::string *label; }; }; |
2、类的定义必不可少
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | class DTree : public Feature_Object_Collection { public: DTree (std::initializer_list<Feature_Object> list) : Feature_Object_Collection (list) {} DTree (Feature_Object_Collection& o) : Feature_Object_Collection (o) {} DTree (const DTree &o) : Feature_Object_Collection (o) {} ~DTree () { release_branch (m_root); } //... } |
这个类里面增加了几个函数,calc用于计算,update_tree用于构建决策树,release_branch用于释放决策树。之后的代码全部在DTree类里面,之后的代码全部在DTree类里面,之后的代码全部在DTree类里面,重要的事情说三遍。
3、计算实现代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | //计算 std::string calc (Feature_Data dat) { if (!m_root) update_tree (); //应该进入哪个分支? std::function<std::string (pDecision_Tree_Branch)> calc_tree = [&calc_tree, &dat] (pDecision_Tree_Branch p) { if (p->feature_index != -1) { decltype(p->child->begin ()) min_match = p->child->begin (); double tmp = dat [p->feature_index]; double min_err = ::fabs (min_match->first - tmp); for (auto i = min_match; i != p->child->end (); ++i) { if (::fabs ((i->first - tmp)) < min_err) { min_err = ::fabs (i->first - tmp); min_match = i; } } return calc_tree (min_match->second); } else { return *(p->label); } }; return calc_tree (m_root); } |
在决策树已经创建的情况下,计算是要简单很多哇。上面代码大致意思是,在决策树里面不停的找合适的分支进行递归,递归结束后返回。
4、构建决策树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | //构建决策树 void update_tree () { if (m_root) release_branch (m_root); ptrdiff_t axis_num = data [0].get_size (); //计算香农熵 auto calc_shannon_entropy = [] (std::vector<pFeature_Object> &dataset) { std::map<std::string, ptrdiff_t> m; for (pFeature_Object &fo : dataset) ++m [fo->get_label ()]; double prob, se = 0.0; for (auto i = m.begin (); i != m.end (); ++i) { prob = i->second / (double) dataset.size (); se -= prob * ::log2 (prob); } return se; }; //切割数据集 auto split_dataset = [] (std::vector<pFeature_Object> &dataset, std::vector<pFeature_Object> &after, ptrdiff_t axis, double value) { after.clear (); for (pFeature_Object &fo : dataset) { if (double_is_equal ((*fo) [axis], value)) after.push_back (fo); } }; //... |
构建的代码虽然不止这么点,但还是比较难以理解。首先是香农熵,这个的概念不太好解释,对此感兴趣的可以在网上找找相关资料,用于计算信息的还有基尼不纯度,这儿就不说这个了,就是香农熵吧。然后是切割数据集。由于决策树在递归构建的时候,内容是不断统一的过程,所以必然涉及到数据集的切割。这儿捡个便宜,就不重新创建数据集了,这儿就用指针数组。反正数据在类里面始终存在不是?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | //... //一串由0和1组成的字符串,长度等于特征个数,1表示已被决策树所使用,0表示未使用 (~ ̄▽ ̄)~ std::string axis_sign (axis_num, '0'); //选择最好的数据划分特征 <( ̄ˇ ̄)/ auto choose_best_feature = [&axis_sign, &calc_shannon_entropy, &axis_num, &split_dataset] (std::vector<pFeature_Object> &dataset) { std::set<double> s; double base_entropy = calc_shannon_entropy (dataset), prob, new_entropy, best_info_gain = -1, info_gain; std::vector<pFeature_Object> after; ptrdiff_t best_feature = -1; for (ptrdiff_t axis = 0, g, size = dataset.size (); axis < axis_num; ++axis) { if (axis_sign[axis] == '1') continue; s.clear (); for (g = 0; g < size; ++g) s.insert ((*dataset [g]) [axis]); new_entropy = 0.0; for (double d : s) { split_dataset (dataset, after, axis, d); prob = after.size () / size; new_entropy += prob * calc_shannon_entropy (after); } info_gain = base_entropy - new_entropy; if (info_gain > best_info_gain || best_info_gain == -1) { best_info_gain = info_gain; best_feature = axis; } } if (best_feature != -1) axis_sign [best_feature] = '1'; return best_feature; }; //... |
以上是数据划分特征,通过香农熵来计算最好的数据划分特征。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | //... //创建决策树分支 std::function<pDecision_Tree_Branch (std::vector<pFeature_Object> &, ptrdiff_t)> create_branch = [&create_branch, &choose_best_feature] (std::vector<pFeature_Object> &dataset, ptrdiff_t feature_num) { pDecision_Tree_Branch ret = new Decision_Tree_Branch; ptrdiff_t i, size = dataset.size (); for (i = 1; i < size; ++i) { if (dataset [i]->get_label() != dataset[0]->get_label()) break; } if (i == dataset.size ()) { ret->feature_index = -1; ret->label = new std::string (dataset [0]->get_label ()); } else { if (feature_num == 1) { std::map<std::string, ptrdiff_t> m; for (pFeature_Object &fo : dataset) ++m [fo->get_label ()]; i = -1; ret->label = new std::string (""); for (auto &t : m) { if (t.second > i) { *ret->label = t.first; i = t.second; } } ret->feature_index = -1; } else { ret->feature_index = choose_best_feature (dataset); std::map<double, std::vector<pFeature_Object>> p; std::map<double, std::vector<pFeature_Object>>::iterator j; for (i = 0; i < size; ++i) { for (j = p.begin (); j != p.end (); ++j) { if (double_is_equal (j->first, (*dataset [i]) [ret->feature_index])) break; } if (j == p.end ()) { p.insert ({ (*dataset [i]) [ret->feature_index], { dataset [i] } }); } else { j->second.push_back (dataset [i]); } } ret->child = new std::map<double, pDecision_Tree_Branch> (); for (j = p.begin (); j != p.end (); ++j) { ret->child->insert ({ j->first, create_branch (j->second, feature_num - 1) }); } } } return ret; }; //... |
以上代码用于创建决策树分支,代码逻辑还是比较清晰吧2333,那我就不写注释了
1 2 3 4 5 6 | //... std::vector<pFeature_Object> dat; for (auto i = data.begin (); i != data.end (); ++i) dat.push_back (&*i); m_root = create_branch (dat, axis_num); } |
这个函数特么终于写完了,接下来就是。。。
5、释放决策树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | protected: //释放分支 static void release_branch (pDecision_Tree_Branch p) { if (p) { if (p->feature_index != -1) { for (auto i = p->child->begin (); i != p->child->end (); ++i) release_branch (i->second); delete p->child; } else { delete p->label; } delete p; } } pDecision_Tree_Branch m_root = nullptr; |
释放的代码不用细究,总的来说就是递归、释放、递归、释放
okay,决策代码如上。现在用决策来解决一个实际问题。有四种物种,鸟类、家禽、鱼类和两栖动物,它们每天的飞翔、游泳、走路时间总和为1,具体时间在代码里面(好巧这数据也是假的)
6、main函数
1 2 3 4 5 6 7 8 9 10 11 | int main(int argc, char* argv[]) { DTree t ({ //fly swim walk { "Bird", { 0.95, 0, 0.05 } }, //鸟类 { "Poultry", { 0.1, 0.45, 0.45 } }, //家禽 { "Fish", { 0, 1, 0 } }, //鱼类 { "Amphibious", { 0, 0.5, 0.5 } } //两栖 }); cout << "Calc value is: " << t.calc ({ 0.03, 0.97, 0 });//飞鱼 return 0; } |
这儿构建的决策树,主节点通过fly特征进行切割,分成3个子节点,鸟类、家禽和不会飞的物种,然后不会飞的物种通过游泳特征进行再次切割,分成鱼类和两栖类。
我这儿执行结果如下所示:
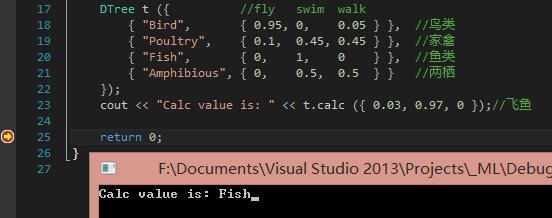
虽然执行速度非常快,但精度不如k-近邻算法,假如飞鱼多飞一会,>0.05之后,就直接被决策为家禽了。